Mathematical joke
A mathematical joke is a form of humor which relies on aspects of mathematics or a stereotype of mathematicians to derive humor. The humor may come from a pun, or from a double meaning of a mathematical term. It may also come from a lay person's misunderstanding of a mathematical concept (which is not wholly unexpected). These jokes are frequently inaccessible to those without a mathematical bent.
Contents |
Pun-based jokes
Some jokes simply use a mathematical term with a second non-technical meaning as the punchline of a joke.
- Q. What's purple and commutes?
- A. An Abelian grape. (A pun on Abelian group.)[1]
Other jokes create a double meaning from a direct calculation involving facetious variable names:
- Person 1: What's the integral of 1/cabin with respect to cabin?
- Person 2: A log cabin.
- Person 1: No, a houseboat; you forgot to add the C!
The first part of this joke relies on the fact that the primitive (formed when finding the antiderivative) of the function 1/x is log|x|. The second part is then based on the fact that the antiderivative is actually a class of functions, requiring the inclusion of a constant of integration, usually denoted as C—something which calculus students may forget. Thus, the indefinite integral of 1/cabin is "log|cabin| + C", or "A log cabin plus the sea", i.e., "A houseboat."
This type of joke was featured in an episode of The Simpsons, "Bart the Genius." Bart cheated on an exam and as a result was placed into a gifted school. However, since he did not have previous exposure to calculus, he was unable to see the humor in this exchange with his teacher:
- So y = r cubed over 3. And if you determine the rate of change in this curve correctly, I think you'll be pleasantly surprised. [The class, except for Bart, laughs] Don't you get it, Bart? Differential dy = 3 r squared dr over 3, or r squared dr, or r dr r.[2]
This joke also relies on knowledge that "hardy har har" (r dr r) is an English onomatopoeia for laughter .
Jokes with numeral bases
- There are only 10 types of people in the world: those who understand binary, and those who don't.
This joke relies on the fact that mathematical expressions, just as expressions in natural languages, may have multiple meanings. Like other puns, the humor is derived from an ambiguous meaning; in this case, the expression 10 in the binary numeral system is equal to the decimal number two.
Another pun using different radices, sometimes attributed to computer scientists, asks:
The humor lies in the similarity of the abbreviation for October/Octal and December/Decimal, and the coincidence that the two representations equal the same amount (31 Octal is 3*8 + 1 = 25 Decimal).
Stereotypes of mathematicians
Some jokes are based on stereotypes of mathematicians tending to think in complicated, abstract terms, causing them to lose touch with the "real world".
Many compare mathematicians to other professions, typically physicists, engineers, or the "soft" sciences in a form similar to an Englishman, an Irishman and a Scotsman. The joke generally shows the other scientist doing something practical, while the mathematician does something less useful such as making the necessary calculation but not performing the implied action.
Examples:
- A physicist, a biologist and a mathematician are sitting in a street café watching people entering and leaving the house on the other side of the street. First they see two people entering the house. Time passes. After a while they notice three people leaving the house. The physicist says, "The measurement wasn't accurate." The biologist says, "They must have reproduced." The mathematician says, "If one more person enters the house then it will be empty."
An example of a joke relying on mathematicians' propensity for not taking the implied action is as follows:
- A mathematician, an engineer and a chemist are at a conference. They are staying in adjoining rooms. One evening they are downstairs in the bar. The mathematician goes to bed first. The chemist goes next, followed a minute or two later by the engineer. The chemist notices that in the corridor outside their rooms is a rubbish bin that is ablaze. There is a bucket of water nearby. The chemist starts concocting a means of generating carbon dioxide in order to create a makeshift extinguisher but before he can do so the engineer arrives, dumps the water on the fire and puts it out. The next morning the chemist and engineer tell the mathematician about the fire. She admits she saw it. They ask her why she didn't put it out. She replies contemptuously "there was a fire and a bucket of water: a solution obviously existed."
The last sentence is also a dig at proofs of existence, which merely show that a certain object must exist but are entirely unhelpful in constructing such an object.
An example of a joke by Bill Bailey highlighting mathematicians' habits of creating hypothetical situations with little real-world applications (such as ad infinitum situations) is as follows:
- An infinite number of mathematicians walk into a bar. The first goes up to the bartender and says, "I'll have a pint of lager, please." Each next one says, "and I'll have half of what he's having." The bartender says, "You're all idiots," and pulls two pints.
This joke also relies on the fact that the infinite sum 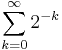 is equal to 2 (and that one wouldn't expect most bartenders to know this).
is equal to 2 (and that one wouldn't expect most bartenders to know this).
Mathematicians are also shown as averse to making sweeping generalizations from a small amount of data, preferring instead to state only that which can be logically deduced from the given information—even if some form of generalization seems plausible:
- An astronomer, a physicist and a mathematician are on a train in Scotland. The astronomer looks out of the window, sees a black sheep standing in a field, and remarks, "How odd. Scottish sheep are black." "No, no, no!" says the physicist. "Only some Scottish sheep are black." The mathematician rolls his eyes at his companions' muddled thinking and says, "In Scotland, there is at least one sheep, at least one side of which appears to be black from here."
Non-mathematician's math
This category of jokes comprises those that exploit common misunderstandings of mathematics, or the expectation that most people have only a basic mathematical education, if any.
Examples:
- A museum visitor was admiring a Tyrannosaurus fossil, and asked a nearby museum employee how old it was. "That skeleton's sixty-five million and three years, two months and eighteen days old," the employee replied. "How can you know it that well?" she asked. "Well, when I started working here, I asked a scientist the exact same question, and he said it was sixty-five million years old—and that was three years, two months and eighteen days ago."
The joke is that the employee fails to understand the scientist's implication of the uncertainty in the age of the fossil and uses false precision.
Mock mathematics
A form of mathematical humor comes from using mathematical tools (both abstract symbols and physical objects such as calculators) in various ways which transgress their intended scope. These constructions are generally devoid of any substantial mathematical content, besides some basic arithmetic.
Mock mathematical reasoning
A set of equivocal jokes applies mathematical reasoning to situations where it is not entirely valid. Many of these are based on a combination of well-known quotes and basic logical constructs such as syllogisms:
Example:
-
Premise I: Knowledge is power. Premise II: Power corrupts. Conclusion: Therefore, knowledge corrupts.
Another set of jokes relate to the absence of mathematical reasoning, or misinterpretation of conventional notation:
Examples:
That is, the limit as x goes to 8 from above is a sideways 8 or the infinity sign, in the same way that the limit as x goes to three from above is a sideways 3 or the Greek letter omega.[3]
The "d's" from the first part of the equation are cancelled out and leave only one over x times x, equaling one. The first and last part of the equation are correct: the derivative of a first degree variable is 1, however the intermediate process is not mathematically sound, as "d" is not an algebraic expression but an operator.
Calculator spelling
Calculator spelling is the formations of words and phrases by entering a number and turning the calculator upside down. The words can be accompanied by stories involving numbers that lead to the solution. For example: 142 workers and 154 civilians fought over 69 oil fields for 5 days. What did they fight over? 14215469 x 5 = 71077345, which, when read upside down, appears roughly to be "ShELL OIL." This only appears correctly when the open top '4' is used by the calculator.
Math limericks
A math limerick is an expression which, when read aloud, matches the form of a limerick. The following example is attributed to Leigh Mercer:[4]
This is read as follows:
- A dozen, a gross, and a score
- Plus three times the square root of four
- Divided by seven
- Plus five times eleven
- Is nine squared and not a bit more.
An example employing integral calculus is written mathematically as
This is read as follows:
- The integral of z squared dz
- From one to the cube root of three
- Times the cosine
- Of three pi over nine
- Equals log of the cube root of e
Donut and coffee mug topology joke
An often-repeated joke is that topologists can't tell a coffee cup from a doughnut,[5] since a sufficiently pliable doughnut could be reshaped (by a homeomorphism) to the form of a cup by creating a dimple and progressively enlarging it, while shrinking the hole into a handle.
See also
Notes
- ^ Weisstein, Eric W., "Abelian Group" from MathWorld.
- ^ Nestler, Andrew. "r dr r". http://homepage.smc.edu/nestler_andrew/math7/rdrr.htm. Retrieved 2010-01-12.
- ^ Xu, Chao (2008-02-21). "A mathematical look into the limit joke". http://mgccl.com/2008/02/21/a-mathematical-look-into-the-limit-joke. Retrieved 2008-04-19.
- ^ "Math Mayhem". Lhup.edu. http://www.lhup.edu/~DSIMANEK/mayhem.htm. Retrieved 2011-06-29.
- ^ Differential Equations: A Dynamical Systems Approach : Higher-Dimensional Systems. Books.google.com. 1995-03-30. http://books.google.com/books?id=SHBj2oaSALoC&pg=PA204&dq=%22coffee+cup%22+topologist+joke&hl=en&ei=Z-SHTLa4CY34swPI99SOCg&sa=X&oi=book_result&ct=result&resnum=3&ved=0CEIQ6AEwAg#v=onepage&q=%22coffee%20cup%22%20topologist%20joke&f=false. Retrieved 2011-06-29.
Further reading
- Paul Renteln and Alan Dundes (2004-12-08). "Foolproof: A Sampling of Mathematical Folk Humor" (PDF). Notices of the AMS 52 (1). http://www.ams.org/notices/200501/fea-dundes.pdf.
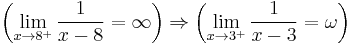
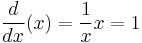
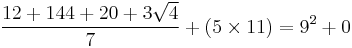
![\left( \int_{1}^{\sqrt[3]{3}} z^2 \; dz \right) \cos\left(\dfrac{3\pi}{9}\right) \; = \; \log\left( \sqrt[3]{e} \right)](/2012-wikipedia_en_all_nopic_01_2012/I/b33fa91ea6c43d134356bf228d9412c1.png)